Angka Penting

A.    ANGKA PENTING

Agar pengukuran dalam fisika tidak terlalu memakan tempat, maka kita dapat menggunakan notasi ilmiah atau notasi baku. Dalam notasi ilmiah, hasil pengukuran dinyatakan sebagai:

      a,… x10ⁿ

a adalah bilangan asli mulai 1 sampai dengan 9, disebut bilangan penting

n adalah eksponen dan merupakan bilangan bulat disebut orde besar

Aturan Angka Penting:

1. Semua angka yang bukan nol adalah angka penting.

 Contoh : Hasil pengukuran 65,89 cm (4 angka penting)

2. Angka nol yang terletak di antara angka bukan nol adalah angka penting.

   Contoh : 1,002 (4 angka penting)

3. Angka nol di sebelah kanan tanda desimal dan tidak diapit angka bukan nol bukan angka penting.

   Contoh :  25,00 (2 angka penting)

25,000 (2 angka penting)

2500 (4 angka penting, mengapa ? sebab tidak ada tanda desimalnya)

4. Bilangan-bilangan puluhan, ratusan, ribuan, dan seterusnya yang memiliki angka-angka nol pada deretan akhir harus dituliskan dalam notasi ilmiah agar jelas apakah angka-angka nol tersebut adalah angka penting atau bukan.

   Contoh :

       Angka terakhir pada contoh di atas bersifat ambigu. Untuk menghilangkan sifat ambigu, notasi ilmiah harus dipakai.

5. Semua angka sebelum orde (Pada notasi ilmiah) termasuk angka penting.

Contoh :  3,2x 10⁵ memiliki dua angka penting, yakni 3 dan 2.

              4,50 x 10³ memiliki tiga angka penting, yakni 4, 5 dan 0.

 6. Angka nol yang berada di belakang angka bukan nol, bukan termasuk angka penting kecuali setelah ditentukan letak desimalnya.

Contoh : angka 12500, harus diubah dulu menjadi 1,25 x 10⁴

berarti memiliki 3 angka penting. Jika kita mengubahnya menjadi

1,250 x 10⁴ berarti terdapat 4 angka penting

 7. Angka nol yang terletak di sebelah kiri angka bukan nol atau setelah tanda desimal bukan angka penting.

Contoh :  0,00556 = 3 angka penting

0,00006500 = 4 angka penting

 8. Batasan jumlah angka penting bergantung dengan tanda yang diberikan pada urutan angka dimaksud. Dengan kata lain, Angka 0 pada deretan akhir sebuah bilangan termasuk angka penting, kecuali kalau angka sebelum 0 diberi garis bawah. Contoh: 1500 ton (memiliki 4 angka penting) tapi kalau ada garis bawah di angka 0 pertama maka angka pentingnya jadi 3.

Contoh Soal:

1. Hitunglah jumlah angka penting pada angka-angka dibawah ini.

a. 1,0050

b. 23,4000

c. 0,010025

d. 13,000124

e. 4500

2. Tulislah bilangan penting, orde besar dan tulislah angka ini dalam notasi ilmiah!

a. 9600 gram

b. 0,00456

Pembahasan:

1. 1. 5 angka penting yakni 1, 0, 0, 5, 0

    2. 6 angka penting yakni 2, 3, 4, 0, 0, 0

    3. 5 angka penting yakni 1, 0, 0, 2, 5

    4. 8 angka penting yakni 1, 3 ,0, 0, 0, 1, 2, 4

    5. 4500 harus diubah dulu menjadi bentuk baku 4,5 x 10³

 jadi ada 2 angka penting yakni 4, 5 namun jika kita mengubahnya menjadi 4,50 x 10³

 maka ada 3 angka penting yakni 4, 5, 0

2. a. 96000000000 gram = 9,6 x 10¹⁰ gram Melewati 10 angka 

Bilangan penting = 9,6

Orde besar = 10¹⁰

b.           0,000456 m = 4,56 x 10^-4 m Melewati 4 angka           

    Bilangan penting = 4,56

         Orde besar = 10^-4

Aturan Penjumlahan dan Pengurangan angka penting

Jika menjumlahkan atau mengurangi dua angka penting atau lebih, maka angka hasil penjumlahan atau pengurangan tidak boleh lebih akurat atau teliti dari angka yang paling tidak akurat atau teliti. Banyaknya jumlah angka penting dalam hasil penjumlahan dan pengurangan tidak berpengaruh.

Contoh soal:

1.      Jumlahkanlah 178,98 g; 12,3 g; dan 67,89 g

  178,98(2 angka dibelakang koma)

  12,3    (1 angka dibelakang koma)

  67       (0 angka dibelakang koma)

  8,28dibulatkan 258 karena hanya boleh mengandung 0 angka dibelakang koma.

Aturan Perkalian dan Pembagian

Jika membagikan atau mengalikan dua angka penting atau lebih, maka hasil perkalian atau pembagian mempunyai jumlah angka penting paling sedikit yang digunakan dalam perkalian atau pembagian tersebut.

Contoh Soal: Selesaikan 4,555 x 10⁵ : 3,0 x 10²

 dengan aturan angka penting!

Pembahasan:

4,555 x 10⁵ kg empat angka penting

5         x 10² m³satu angka penting

-------------------------  :

0,911  x 10³ kg/m³dibulatkan menjadi 0,9 x 10³ kg (satu angka penting)

B.     PENGUKURAN

Pengukuran atau “mengukur” adalah sebagai suatu kegiatan membandingkan suatu besaran dengan besaran lain yang ditetapkan sebagai standar satuan. Untuk melakukan pengukuran sauatu besaran fisika kita memerlukan suatu alat ukur.

BESARAN DAN ALAT UKUR

BESARAN POKOK	ALAT UKUR
Panjang	Mistar, jangka sorong, mikrometer sekrup
Massa	Neraca (Timbangan)
Waktu	Stopwatch
Suhu	Termometer
Kuat Arus Listrik	Amperemeter
Jumlah Molekul	Tidak diukur secara langsung*
Intensitas Cahaya	Lightmeter

*Untuk mengetahui jumlah zat, terlebih dahulu diukur massa zat tersebut.

1.      MISTAR

Mistar digunakan untuk mengukur suatu panjang benda mempunyai batas ketelitian 0,5 mm.

2.      JANGKA SORONG

Jangka sorong digunakan untuk mengukur suatu panjang benda mempunyai batas ketelitian 0,1 mm.

3.      MIKROMETER SEKRUP

Mikrometer sekrup digunakan untuk mengukur suatu panjang benda mempunyai batas ketelitian 0,01 mm.

4.      NERACA

Neraca digunakan untuk mengukur massa suatu benda.

5.      STOPWATCH

Stopwatch digunakan untuk mengukur waktu mempunyai batas ketelitian 0,01 detik.

6.      TERMOMETER

Termometer digunakan untuk mengukur suhu. 

7.      AMPEREMETER

Amperemeter digunakan untuk mengukur kuat arus listrik (multimeter)

Contoh Soal:

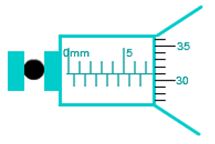
1.       Sebuah balok diukur ketebalannya dengan jangka sorong. Skala yang ditunjukkan dari hasil pengukuran tampak pada gambar. Besarnya hasil pengukuran adalah...

2.       Jika kita menggunakan mistar atau penggaris, maka ketidakpastiannya adalah...

3.       Suatu benda berbentuk bola kecil diukur diameternya menggunakan mikrometer skrup seperti terlihat pada gambar di bawah ini.

cara membaca skala mikrometer skrup Bacaan skala yang tepat dari pengukuran diameter benda tersebut adalah .....

Pembahasan:

1.       Skala utama = 3,1 cm
Skala nonius = 9 x 0,01 = 0,09 cm
Tebal balok = 3,1 cm + 0,09 cm = 3,19 cm

2.      Pengukuran tunggal merupakan pengukuran yang dilakukan satu kali saja. Ketidakpastian pada pengukuran tunggal dapat ditentukan dengan rumus berikut :

Δx = ½ x skala terkecil .

Skala terkecil pada mistar adalah 0,1 cm. Dengan demikian, ketidakpastian pada pengukuran tunggal dengan menggunakan mistar adalah :

⇒ Δx = ½ x skala terkecil

⇒ Δx = ½ (0,1)

⇒ Δx = 0,05 cm.

3.      Pada mikrometer skrup ada dua skala yaitu skala utama dan skala nonius. Panjang benda yang diukur merupakan jumlah dari skala utama dan skala nonius. x = skala utama + skala nonius Cara Membaca Mikrometer Skrup Untuk membaca skala pada mikrometer skrup perhatikan garis yang berhimpit pada skala nonius dan garis mendatar pada skala utama. Untuk lebih jelasnya perhatikan gambar di bawah ini.

Dari gambar di atas, jelas terlihat bahwa skala nonius dan garis skala utama berhimpit pada 0,31 mm (31 x 0,01) sedangkan skala utama menunjukkan 7 mm. Dengan demikian panjang diameter benda yang diukur adalah :

⇒ d = skala utama + skala nonius

⇒ d = 7,00 + 0,31

⇒ d = 7,31 mm.